
Новый Эталон Килограмма
может в ближайшее время заменить устаревший платиново-иридиевый... »»»

Солнце Становится Ближе
получены изображения высокого разрешения Солнца с космической обсерватории Solar Dynamics Observatory... »»»

Человек "Искрививший" Время
биография Альберта Эйнштейна - величайшего физика создавшего "Общую теорию относительности"... »»»

Что за Очки у Будущего?
история создания, развития и будущее популярного оптического прибора... »»»
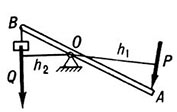 Одним из важных практических применений моментов сил относительно точки являются простые «механизмы», такие, как рычаг. «Механизмы» здесь — это любое приспособление, позволяющее силе, приложенной в одной точке, уравновесить или преодолеть другую силу в другой точке. Приложенная сила называется усилие Е, а сила, которую «механизм» должен преодолеть, известна как нагрузка L.
Одним из важных практических применений моментов сил относительно точки являются простые «механизмы», такие, как рычаг. «Механизмы» здесь — это любое приспособление, позволяющее силе, приложенной в одной точке, уравновесить или преодолеть другую силу в другой точке. Приложенная сила называется усилие Е, а сила, которую «механизм» должен преодолеть, известна как нагрузка L.
Механическая выгода
Отношение нагрузки L и усилия Е известно как механическая выгода (МА — англ.; MB — рус.) «механизма». Таким образом, МВ = (нагрузка L, Н) / (усилие Е, Н) и, следовательно, не имеет размерности. Груз весом 100 Н поднят вследствие приложения усилия 20 Н к «механизму». Механическая выгода L/E = 100 Н:20 Н = 5. «Механизмы» могут иметь значение MB, равное 1, больше чем 1 и даже меньше 1.
Простой неподвижный блок имеет MB ≈ 1, и здесь выгода состоит в изменении направления приложения силы: вниз более удобно для работы вместо вверх (менее удобно). Строение человеческого скелета позволяет с большей легкостью прилагать силы, направленные вниз, нежели силы, направленные вверх. Велосипед является типичным примером «механизма», имеющего МВ < 1. Здесь преимущество состоит в том, что велосипедист может управлять велосипедом более легко, чем если бы он имел МВ > 1. Одним из преимуществ использования большего усилия, чем нагрузка, является процесс увеличения скорости. Другое преимущество состоит в том, что велосипедист может ехать на «свободных колесах», не нажимая на педали по склону или по ровному участку дороги, и экономить силы. Большинство «механизмов» имеет МВ > 1, и именно они дают настоящую выгоду при использовании.







