
Новый Эталон Килограмма
может в ближайшее время заменить устаревший платиново-иридиевый... »»»

Солнце Становится Ближе
получены изображения высокого разрешения Солнца с космической обсерватории Solar Dynamics Observatory... »»»

Человек "Искрививший" Время
биография Альберта Эйнштейна - величайшего физика создавшего "Общую теорию относительности"... »»»

Что за Очки у Будущего?
история создания, развития и будущее популярного оптического прибора... »»»
 Когда вы вычертили график, вам часто требуется выявить градиент (или наклон) прямой линии или кривой в определенной точке.
Когда вы вычертили график, вам часто требуется выявить градиент (или наклон) прямой линии или кривой в определенной точке.
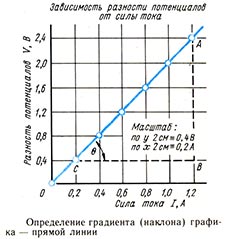
Определение градиента прямолинейного графика
Прямолинейный график на рисунке изображает зависимость между разностью потенциалов V и силой тока / для некоторого резистора с постоянным сопротивлением.
Градиент (наклон) прямой, изображающей эту зависимость, равен тангенсу угла между прямой и горизонталью, т. е. tg. В этом случае тангенс угла наклона прямой дает сопротивление резистора. Чтобы определить градиент, начертите прямоугольный треугольник в любом месте прямой таким образом, чтобы эта прямая совпадала с гипотенузой. Сделайте треугольник возможно большим для обеспечения наибольшей точности.
Таким образом, сопротивление резистора равно 2,0 Ом. Значения у для точек А (2,4) и В (0,4) следует читать на оси у; линейка, помещенная параллельно оси х в точках А и В, поможет определить это точно. Обратите также внимание, что единица измерения указана на оси у вместе с названием физической величины.
Точно так же точки В (1,2) и С (0,2) считываются с оси х с помощью линейки, расположенной параллельно оси у: единица измерения также отмечена на оси х.
Точки В и С должны быть подобраны обдуманно, т. е.,например, так, как показано на рисунке: ВС = 1,0 — удобное число для деления. Включение единиц измерения точек В и А в формулу и представление их как В-A дает возможность записать градиент (наклон) прямой на графике, соответствующий сопротивлению R резистора в омах (Ом).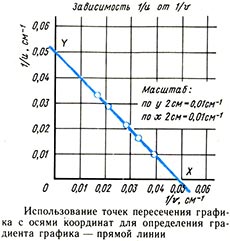
Другую полезную информацию можно получить от точек пересечения прямолинейного графика с осями х и у. Использование точек пересечения может быть проиллюстрировано на графическом изображении формулы собирающей линзы. Формула, связывающая расстояние от линзы до предмета и, расстояние от линзы до изображения и и расстояние от линзы до фокальной плоскости.
Обратите внимание, что в этом примере наклон прямой линии вниз и вправо и, следовательно, градиент (наклон) линии является отрицательным.
Определение градиента в точке Р на кривой
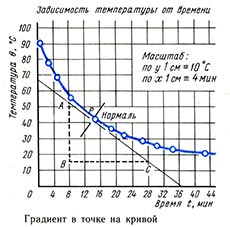 Сначала следует провести касательную к кривой в точке Р (рис. 0.9). Поставьте обычное зеркало вертикально поперек кривой таким образом, чтобы поверхность, покрытая амальгамой, располагалась точно на точке Р. Поворачивайте зеркало вокруг вертикальной оси до тех пор, пока кривая перед зеркалом не станет неразрывной с ее отражением в зеркале. Не сдвигая зеркала, прочертите прямую линию вдоль его края со стороны амальгамы через точку Р. Эта линия является нормалью по отношению к кривой в точке Р. Теперь проведите линию, перпендикулярную к нормали. Эта линия — искомая касательная к кривой в точке Р. Обратите внимание, что градиент (наклон) касательной в точке Р отрицательный.
Сначала следует провести касательную к кривой в точке Р (рис. 0.9). Поставьте обычное зеркало вертикально поперек кривой таким образом, чтобы поверхность, покрытая амальгамой, располагалась точно на точке Р. Поворачивайте зеркало вокруг вертикальной оси до тех пор, пока кривая перед зеркалом не станет неразрывной с ее отражением в зеркале. Не сдвигая зеркала, прочертите прямую линию вдоль его края со стороны амальгамы через точку Р. Эта линия является нормалью по отношению к кривой в точке Р. Теперь проведите линию, перпендикулярную к нормали. Эта линия — искомая касательная к кривой в точке Р. Обратите внимание, что градиент (наклон) касательной в точке Р отрицательный.







