Сайт по физике

В течение многих столетий, наблюдая за вращением Земли вокруг своей оси, определяли точное время. Для того, чтобы правильно работали любые часы необходим постоянный период колебания, например, маятника. Однако, при появлении первых кварцевых часов, человечество обнаружило, что часы идут не совсем точно, как хотелось бы.

Во-первых, со временем наша планета постепенно стала вращаться чуть дольше из-за трения волн приливов и отливов. И через сотню лет ее вращение вокруг своей оси увеличится на  0,00164 секунды. Во-вторых,  Земля вращается не равномерно: то быстрее, то медленнее, в результате длина каждого дня тоже изменяется на 0.001 секунды. Одинаково равномерно в наши дни Земля перестала вращаться, поэтому это не может быть эталоном времени.

Несовершенство естественных природных часов заставило человека создавать искусственные приборы, способные более точно выполнять функции определения времени, часы. На сегодняшний день любой человек хоть что-то знает о часах, но не все знают о том, что часы являются сегодня самым массовым измерительным прибором. В год производится более 300 миллионов штук часов, а измерение времени на  Земле ежедневно производится несколько десятков миллиардов раз.

   При проведении исследования - проверка на практике закона Архимеда, можно использовать прибор, показанный на рисунке. Подвесьте при помощи тонкой нити на пружинные весы твердое тело, например брусок металла. Запишите вес W₁ твердого тела. Используемый брусок должен давать растяжение, близкое к максимальному для применяемых весов. Наполните отливной сосуд водой до уровня стока, соберите и удалите излишки воды, вылившейся через сток. Поместите чистый сухой лабораторный стакан на весы и запишите его вес w₁. Затем осторожно опустите висящее на весах твердое тело в отливной сосуд так, чтобы часть его погрузилась в воду.

   Хотя вес W₁твердого тела не изменился, показание W₂ на пружинных весах дает кажущееся уменьшение веса. Эта видимая потеря веса является следствием действия направленной вверх выталкивающей силы U₁, действующей на твердое тело вследствие вытеснения им воды.

Представим себе пробку, которая погружается под поверхность воды в сосуде (рис. 3.14).  Силами,   действующими на пробку, являются сила тяжести W и сила давления F вниз пальца плюс выталкивающая сила U₁ воды. Если пробка неподвижна, то W + F = U₁. Поскольку U₁>W, то ре­зультирующая этих двух сил, направ­ленная вверх (U₁ — W), заставит пробку ускоряться вверх, когда палец уб­ран. Постепенно пробка придет в сос­тояние покоя в частично погруженном в воду положении. Это произойдет при U₂=W, т. е. когда выталкиваю­щая сила U₂ станет равна весу пробки. Архимед исследовал закономерности плавания тел и обнаружил зависи­мость, известную как закон Архиме­да.

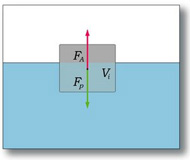
Теперь давайте перейдем от сил в твердых телах к силам в жидкостях. Если твердое тело погружается в жид­кость, то оно будет вытеснять жид­кость и в результате жидкость будет оказывать ответное давление на твер­дое тело. Это пример третьего закона движения Ньютона, который утверж­дает, что действие и противодействие равны и противоположны. Исходящая от жидкостей направленная вверх си­ла, действующая на объекты, поме­щенные в жидкость, известна как выталкивающая сила. Выталкиваю­щая сила действует на тело в жид­кости, даже если это тело закрепле­но на какой-то опоре, такой, как, например, дно сосуда. Мраморный шарик, брошенный в воду, находя­щуюся в сосуде, погрузится на его дно, как показано на рисунке 3.13, а.

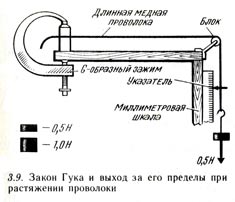
Зажмите один конец тонкой медной про­волоки длиной от 2 до 3 м и перекиньте ее через легко вращающееся колесико блока, как показано на рисунке. Присоедините  груз весом 0,5 Н к другому концу проволоки, для того чтобы она натянулась. Затем присоеди­ните к проволоке указатель так, чтобы он на­ходился рядом с миллиметровой шкалой.

До­бавляйте к висящему грузу различные гирьки порциями, например весом по 0,5 Н, и отме­чайте растяжение для каждого груза. В этом исследовании вы можете нагружать  проволоку до ее предела упругости и выше его, пока проволока не порвется.

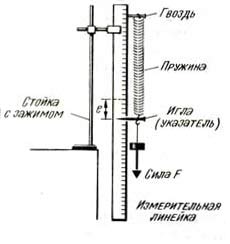
Соберите прибор, как показано на рисун­ке 3.7, а. Установите иглу на нижнем конце пружины, чтобы она действовала как указа­тель, и отметьте положение указателя на из­мерительной линейке при отсутствии прило­женной силы. Этот произвольный нуль дол­жен быть проверен в конце эксперимента, чтобы удостовериться, что максимальная сила, приложенная к пружине, не превысила пре­дел упругости. Прикрепите крюк для взвеши­вания (к которому подвешиваются грузы с известной массой) к нижнему концу пружины. Когда пружина перестанет колебаться, отметь­те новое положение указателя. Разность двух показаний дает растяжение е, которое может быть выражено в мм. Присоединяйте гирьки, например, весом по 0,5 Н к крюку (вес кото­рого также равен 0,5 Н), чтобы сила, растя­гивающая пружину, могла увеличиваться от нуля до 3 Н порциями по 0,5 Н.

Взаимосвязь между растяжением спиральной пружины и приложенной силой впервые была исследована Ро­бертом Гуком и известна как закон Гука. Закон Гука утверждает, что для спиральной пружины или другого упругого материала растяжение е прямо пропорционально приложенной силе F, если не преодолен предел упру­гости.

Предел упругости определяет­ся максимальной силой, при которой еще не получаются остаточные дефор­мации (остающиеся в теле после сня­тия нагрузки). При силах, не дохо­дящих до предела упругости, пружина возвращается к своей исходной длине или   форме   после   снятия   нагрузки.