Новый Эталон Килограмма
может в ближайшее время заменить устаревший платиново-иридиевый... »»»
Солнце Становится Ближе
получены изображения высокого разрешения Солнца с космической обсерватории Solar Dynamics Observatory... »»»
Человек "Искрививший" Время
биография Альберта Эйнштейна - величайшего физика создавшего "Общую теорию относительности"... »»»
Что за Очки у Будущего?
история создания, развития и будущее популярного оптического прибора... »»»
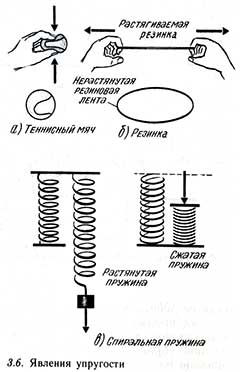
Взаимосвязь между растяжением спиральной пружины и приложенной силой впервые была исследована Робертом Гуком и известна как закон Гука. Закон Гука утверждает, что для спиральной пружины или другого упругого материала растяжение е прямо пропорционально приложенной силе F, если не преодолен предел упругости.
Предел упругости определяется максимальной силой, при которой еще не получаются остаточные деформации (остающиеся в теле после снятия нагрузки). При силах, не доходящих до предела упругости, пружина возвращается к своей исходной длине или форме после снятия нагрузки.
Пружинные весы
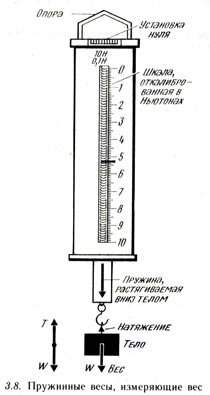
Одним из важных практических применений этого закона являются пружинные весы (рис. 3.8). Это компактный вариант прибора, примененный в описанном выше исследовании. Пружина и стрелка собраны в корпусе, который имеет отградуированную шкалу. Нулевое показание стрелки весов может регулироваться. Эти весы имеют крюк, за который их можно повесить, и еще один крюк, на который помещается тело для взвешивания. Предположим, что на весы подвешено некоторое тело. Притяжение этого тела Землей заставляет его растягивать пружину с силой, которая равна его весу; сила, отмеченная пружинными весами,— это вес W тела.
Когда вы должны взвесить какое-нибудь тело, т. е. измерить силу тяжести, действующую на него, то вам нужно воспользоваться пружинными весами. В вашей лаборатории вы наверняка сможете найти пружинные весы, которые отградуированы в граммах или килограммах, т. е. в единицах измерения массы, а не силы. Поскольку вес W тела массой m определяется по формуле W = mg и W = const x е для пружины, то mg = const x e, откуда m=const / g x e.
Таким образом, для определенного значения g m пропорционально е. Поэтому массы тел могут сравниваться при помощи пружинных весов. Если пружинные весы применяются для взвешивания тела массой m в двух разных географических точках, необходимо учесть, что g в них может быть разным. Это даст два различных веса W1=mg1 и W2 = mg2. В первом месте m = W1/g1, а во втором месте, где были применены весы, m =W2/g2. Из этого следует, что для получения значения массы при помощи пружинных весов сила W2 должна быть разделена на g2, местное значение ускорения свободного падения. Проще было бы использовать подвесные или рычажные весы!
Поведение проволоки может быть объяснено, исходя из молекулярной теории. Рисунок 3.11 показывает упрощенный вариант закономерности, как изменяются силы взаимодействия между двумя молекулами с изменением расстояния между ними. На расстоянии одного диаметра молекулы электрические силы уравновешены, и поэтому результирующая сила равна нулю.
Молекулы в металлической проволоке колеблются около некоторых положений, расстояния между которыми для данной температуры примерно равны диаметру молекулы. Если молекулы сближаются, то возникает мощная сила отталкивания, которая стремится развести их врозь. Именно поэтому твердое тело трудно сжать. Наоборот, если молекулы расходятся на расстояние, превышающее один диаметр молекулы, то возникает сила притяжения, которая стремится свести их ближе друг к другу, отсюда понятно, почему трудно растянуть проволоку.
Когда к проволоке приложена растягивающая сила, молекулы расходятся друг от друга и сила притяжения между молекулами возрастает и становится равной по модулю этой растягивающей силе. Если растягивающая сила устраняется, внутримолекулярные силы притяжения приводят проволоку в ее исходную форму. Силы притяжения, однако, способны действовать на коротком расстоянии, и поэтому, когда растяжение существенно увеличивается, но не достигает значения в точке Y, молекулярные слои смещаются друг относительно друга и происходит необратимое изменение во внутренней структуре проволоки. Деформация, как говорят, становится пластической, и разгрузка проволоки не восстанавливает ее исходную длину.
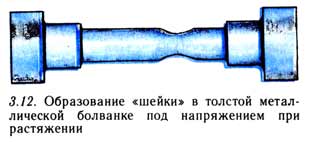Для того чтобы растянуть короткий толстый металлический стержень до разрыва, применяется устройство под названием тензометр. Когда к металлу приложены чрезвычайно большие силы, он начинает утончаться в центре (рис. 3.12).
деформация тела, инерциальная система отсчета,закон сохранения энергии
