
Новый Эталон Килограмма
может в ближайшее время заменить устаревший платиново-иридиевый... »»»

Солнце Становится Ближе
получены изображения высокого разрешения Солнца с космической обсерватории Solar Dynamics Observatory... »»»

Человек "Искрививший" Время
биография Альберта Эйнштейна - величайшего физика создавшего "Общую теорию относительности"... »»»

Что за Очки у Будущего?
история создания, развития и будущее популярного оптического прибора... »»»

Сила — это действие одного тела на другое, причина ускорения. В единицах СИ она выражается в ньютонах (Н). Каждый объект имеет массу и, таким образом, притягивается к Земле силой гравитационного притяжения. Если тело, находящееся на некоторой высоте над Землей, отпустить, то оно начнет падать, т. е. двигаться по направлению к земной поверхности с постоянным ускорением, известным под названием ускорение свободного падения g. В общем случае результирующая сила F, действуя на тело массой m, заставляет его двигаться с ускорением а, т. е. F = ma.
Единицей измерения силы является кг-м-с-2, она названа ньютоном и обозначается Н.
Когда тело падает свободно, ускорение — это g, а сила, действующая на тело, известная как вес W дается формулой W = mg. Вес данного тела будет изменяться, если изменяется g. Небольшие различия g наблюдаются в разных географических точках Земли. Два фактора влияют на g: а) форма Земли; б) вращение Земли.
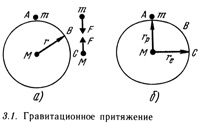
Сначала представим Землю как неподвижный шар (рис. 3.1, а). Сила тяготения F между Землей (масса М) и объектом (масса m) определяется формулой: F=GMm/r2
где r — радиус Земли. Константа G известна под названием универсальная гравитационная постоянная и чрезвычайно мала. Когда r постоянен, сила F — const • m. Притяжение Землей тела массой m определяет вес этого тела: W = mg сравнение уравнений дает: g = const = GM/r2.
Притяжение Землей тела массой m заставляет его падать «вниз» с ускорением g, которое постоянно во всех точках A, В, С и повсюду на земной поверхности (рис. 3.1,6).
Диаграмма сил свободного тела также показывает, что существует сила, действующая на Землю со стороны тела массой m, которая направлена противоположно силе, действующей на тело со стороны Земли. Однако масса М Земли так велика, что «направленное вверх» ускорение а' Земли, вычисляемое по формуле F = Ma', незначительно и им можно пренебречь. Земля имеет форму, отличную от шарообразной: радиус на полюсе rр меньше радиуса на экваторе rе. Это означает, что сила притяжения тела массой m на полюсе Fp=GMm/r2p больше, чем на экваторе Fe= GMm/re. Поэтому ускорение свободного падения gp на полюсе больше ускорения свободного падения ge на экваторе. Ускорение g изменяется с широтой в соответствии с изменением радиуса Земли.
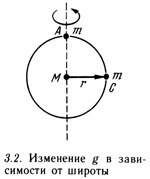
Как вы знаете, Земля находится в постоянном движении. Она вращается вокруг своей оси, совершая один оборот каждые сутки, и движется по орбите вокруг Солнца с оборотом в один год. Принимая для упрощения Землю за однородный шар, рассмотрим движение тел массой m на полюсе А и на экваторе С (рис. 3.2). За одни сутки тело в точке А поворачивается на 360°, оставаясь на месте, в то время как тело, находящееся в точке С, покрывает расстояние в 2лг. Для того чтобы тело, находящееся в точке С, двигалось по круговой орбите, нужна какая-то сила. Это центростремительная сила, которая определяется по формуле mv2/r, где v — скорость тела на орбите. Сила гравитационного притяжения, действующая на тело, находящееся в точке С, F = GMm/r должна:
а) обеспечивать движение тела по окружности;
б) притягивать тело к Земле.
Таким образом, F = (mv2/r)+mg на экваторе, a F = mg на полюсе. Это означает, что g изменяется с изменением широты по мере того, как радиус орбиты изменяется от r в точке С до нуля в точке А.
Интересно представить, что бы случилось, если бы скорость вращения Земли увеличилась настолько, что центростремительная сила, действующая на тело на экваторе, стала бы равной силе притяжения, т. е. mv2/r = F = GMm/r2. Общая гравитационная сила использовалась бы исключительно для удержания тела в точке С на круговой орбите, и не осталось бы силы, действующей на поверхность Земли. Любое дальнейшее увеличение скорости вращения Земли позволило бы телу «уплыть» в пространство. Вместе с тем если космический корабль с астронавтами на борту запущен на высоту R над центром Земли со скоростью v, такой, что выполняется равенство mv*/R=F = GMm/R2, то этот космический корабль будет вращаться вокруг Земли в условиях невесомости.
Точные измерения ускорения свободного падения g показывают, что g изменяется с изменением широты, как показано в таблице 3.1. Отсюда следует, что вес некоторого тела изменяется над поверхностью Земли от максимума на широте 90° до минимума на широте 0°.
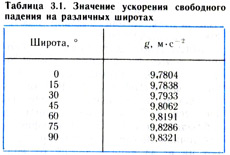
На этом уровне обучения обычно пренебрегают небольшими изменениями в ускорении g и используют среднюю величину 9,81 м-с 2. Для упрощения расчетов ускорение g часто принимают за ближайшее целое число, т. е. 10 м-с-2, и, таким образом, сила притяжения, действующая со стороны Земли на тело массой 1 кг, т. е. вес, принимается за 10 Н. Большинство экзаменационных комиссий для экзаменуемых предлагает использовать с целью упрощения вычислений g=10 м-с-2 или 10 Н-кг-1'.

сила тяжести, закон сохранения импульса, первый закон Ньютона







