
Новый Эталон Килограмма
может в ближайшее время заменить устаревший платиново-иридиевый... »»»

Солнце Становится Ближе
получены изображения высокого разрешения Солнца с космической обсерватории Solar Dynamics Observatory... »»»

Человек "Искрививший" Время
биография Альберта Эйнштейна - величайшего физика создавшего "Общую теорию относительности"... »»»

Что за Очки у Будущего?
история создания, развития и будущее популярного оптического прибора... »»»
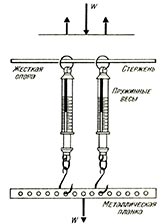 На длинном металлическом стержне подвесьте двое пружинных весов, а к весам подвесьте металлическую планку с отверстиями, просверленными через равные интервалы, как показано на рисунке. Изменяйте положение стержня и расстояние между пружинными весами, снимая показания весов для каждого положения. Где бы ни находился стержень — сумма показаний весов равна весу W металлической планки.
На длинном металлическом стержне подвесьте двое пружинных весов, а к весам подвесьте металлическую планку с отверстиями, просверленными через равные интервалы, как показано на рисунке. Изменяйте положение стержня и расстояние между пружинными весами, снимая показания весов для каждого положения. Где бы ни находился стержень — сумма показаний весов равна весу W металлической планки.
При однородной металлической планке весом W возможно, что: а) каждые из пружинных весов покажут вес W/2; б) пружинные весы покажут неравные части W; в) одни весы покажут значение W, другие 0. Даже если подвесить на металлическую планку дополнительные грузы, то показания весов засвидетельствуют, что сумма сил, направленных вверх, всегда равна сумме сил, направленных вниз, и сумма моментов сил относительно любой точки равна нулю.
Особый случай (в), в котором одни пружинные весы поддерживают планку в равновесии, заслуживает углубленного рассмотрения. Существует только одна точка на планке, в которой одни пружинные весы могут поддерживать ее в равновесии. Понятно, что только одна сила — натяжение пружины весов — приложена к планке в направлении вверх в ее центре. Для равновесия равная и противоположная сила должна также действовать в той же точке. Поэтому будет казаться, что весь вес однородной металлической планки действует в ее средней точке. Вместе с тем известно, что вес распределяется равномерно по длине однородной планки. Если два одинаковых малых груза подвешены на планке так, что они равно удалены от центра, то планка остается в равновесии и дружинные весы показывают общий вес (W = 2ω).
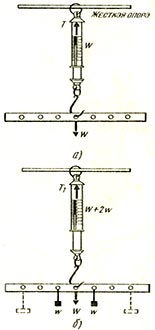
Тот же эффект достигается, если два груза весом w каждый подвешены в центре планки. Таким образом, две равные параллельные силы, действующие в одном направлении, имеют результирующую силу, равную сумме этих сил и действующую в точке, находящейся посередине между точками приложения этих сил. Результат подтверждается при добавлении других пар грузов равного веса к планке. Теперь должно быть понятно, почему общий вес планки W (см. рис), а помещен в центре ее на диаграмме. Представим, что металлическая планка сделана из десяти равных частей, каждая весом w. Складывая попарно силы с каждой стороны от центральной точки. Р, нетрудно понять, что результирующая сила равна 10ω, т. е. весу W планки, приложенному в точке Р. Каждая пара сил не произведет вращающего эффекта, потому что моменты сил относительно точки Р всегда сбалансированы. Рисунок показывает диаграмму сил для планки на весах, при этом сила натяжения пружины Т равна и противоположна весу W, обе силы приложены в одной точке Р.
Точно так же возможно определить для всех тел точку приложения равнодействующей всех сил тяжести, каждой из частей данного тела. Эта одна точка известна как центр тяжести тела, и он обычно обозначается на диаграмме буквой «G». Это понятие чрезвычайно важно при решении задач, связанных с реальными телами, имеющими физическую форму, и, следовательно, с распределением веса по всей этой форме. Его использование дает возможность считать, что сила, равная общему весу W тела, приложена в точке О, центре тяжести тела, и пренебречь формой и размерами тела. Пружинные весы с подвешенной на них металлической планкой, а могут быть заменены двумя вертикальными стрелками, характеризующими Т и W, действующими в точке Р. Горизонтальная линия, представляющая положение планки, может быть опущена. Если, однако, на планку действуют другие внешние силы, то горизонтальная линия будет полезной для того, чтобы показать, как и где эти силы действуют.
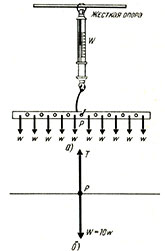
Теперь рассмотрим однородную измерительную линейку, т. е. такую, в которой масса равномерно распределена по ее длине. Линейка «подразделенная» на четыре равных пронумерованных отрезка, каждый из них массой m.
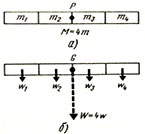
При расчетах в статике и динамике полагают, что общая масса М линейки сконцентрирована в точке Р, и эта точка известна как центр масс.
Cила притяжения Земли, действующую на каждый из отрезков массами m1, m2, m3, m4, придавая им веса ω1, ω2, ω3, ω4 соответственно. При значении g, одинаковом для каждого отрезка, ω = m1g = ω2 = ω3 = ω4 и результирующая этих параллельных сил — это вес W, как и прежде приложенный в центре тяжести G. Итак, если g не изменяется вдоль длины линейки, то центр тяжести G совпадает с центром масс Р. Это в целом будет соответствовать действительности для работы на этом уровне обучения, но в дальнейшем станет ясно, что это не всегда так. Если тело очень велико, то значение g может изменяться вдоль тела и поэтому распределение веса может быть неравномерно при равном распределении массы. Следовательно, положение центра тяжести может отличаться от положения центра масс.
Изменение значения g не рассматривается на этой стадии обучения, и поэтому положение центра масс и центра тяжести будем считать совпадающими. Центры тяжести (или центры масс) некоторых пластин правильной формы показаны на рисунке. Заметьте, что G может быть или внутри тела, или возле него. По этой причине неправильно говорить, что центр тяжести — это точка, на которой тело уравновешивается. Если пластина имеет неправильную форму, ее центр тяжести не может быть найден простым построением линий для определения G. Тут нужен другой способ.







