
Новый Эталон Килограмма
может в ближайшее время заменить устаревший платиново-иридиевый... »»»

Солнце Становится Ближе
получены изображения высокого разрешения Солнца с космической обсерватории Solar Dynamics Observatory... »»»

Человек "Искрививший" Время
биография Альберта Эйнштейна - величайшего физика создавшего "Общую теорию относительности"... »»»

Что за Очки у Будущего?
история создания, развития и будущее популярного оптического прибора... »»»
 Ранее вы узнали, что гравитационный потенциал увеличивается в зависимости от высоты над поверхностью Земли.
Ранее вы узнали, что гравитационный потенциал увеличивается в зависимости от высоты над поверхностью Земли.
Когда тело массой m поднято на высоту h, то совершена работа по преодолению гравитационного поля. Сила mg «работала» на расстоянии h, и совершенная работа равна mgh. Это является увеличением потенциальной энергии тела.
Похожие идеи используются в изучении электричества. Здесь двигающимся телом является варяд. Работа направлена на преодоление электрических сил поля, когда заряд переходит от нижнего уровня потенциала до более высокого. Разность между двумя уровнями называется разностью потенциалов (р.п.), и она выражается в вольтах (В). Если при перемещении заряда в один кулон между двумя точками совершена работа в один джоуль, то разность потенциалов между этими двумя точками составляет один вольт.
Примечание.
Это является определением вольта.
Отсюда следует, что если заряд 2 Кл переместился между двумя точками, то работа равна 2 Дж; если заряд 3 Кл переместился через разность потенциалов 2В, то работа равна 6 Дж. Совершенная работа и затраченная энергия, таким образом, являются произведением заряда и напряжения:
джоуль = кулон *вольт
W = QV.
Это может быть преобразовано в V=W/Q, и поэтому разность потенциалов может быть определена как энергия на единицу заряда. Поскольку также Q = I/t, то подстановка Q дает V=W/It, или V = W/t * 1/I
W/t — это мощность тока, и поэтому разность потенциалов может быть определена также как мощность тока на силу тока.
Возвращаясь к аналогичным положениям гравитационной теории, можно сказать, что любое тело, имеющее возможность перемещаться под воздействием гравитации, будет перемещаться от более высокого уровня к более низкому, например, мяч, выпущенный с вершины склона, катится до дна лощины. Точно так же заряд, имеющий возможность перемещаться под воздействием электрического поля, движется от более высокого потенциала до более низкого.
Примечание.
Это относится к движению положительного заряда.
Таким образом, если разность потенциалов приложена к двум точкам на проводнике, то наблюдается движение заряда.
Закон Ома
Немецкий физик Георг Ом установил, что сила тока I в проводнике пропорциональна разности потенциалов V между его концами, если физические условия, такие, как температура, остаются постоянными, т. е.
I ~ V или V/I = const = R
V = IR
R является коэффициентом пропорциональности и называется сопротивлением проводника. Это соотношение известно как закон Ома. Если V выражается в вольтах, а I — в амперах, то сопротивление R выражается в омах (Ом).
В хорошем проводнике небольшая разность потенциалов V образует большой ток I, следовательно, V/I мало и R мало. Хороший проводник имеет малое сопротивление. С другой стороны, некоторые сплавы, такие, как нихром и константан, имеют достаточно высокое сопротивление, и именно из них изготовляются резисторы. Если бы элемент электрического утюга или электронагревателя был сделан из хорошего проводника, то они бы не работали.
Формула V = IR для определения I или R могла бы быть преобразована в I= V/R или в R = V/I, когда другие переменные известны. Одним из способов для запоминания этих формул является использование треугольника, изображенного на рисунке 25.4. Чтобы получить формулу для данной величины, прикройте нужную букву (скажем, V). Остаются две смежные буквы –I и R, и, следовательно, формула
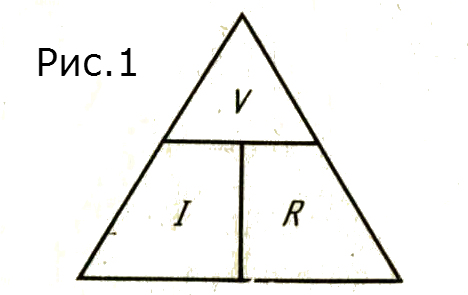
для V представляет собой IR. Если вы прикроете I, то у вас останется V над R, и, следовательно, формулой для I будет V/R, аналогично R — V/I. Этот способ может быть применен к любой формуле, которая содержит три переменные, например Q = It и W = QV. Убедитесь, что вы расположили их в правильных углах треугольника!
Иногда неудобно применять единицы вольт, ампер и ом, и тогда используются их кратные единицы. Некоторые широко употребляемые из них даны в таблице.

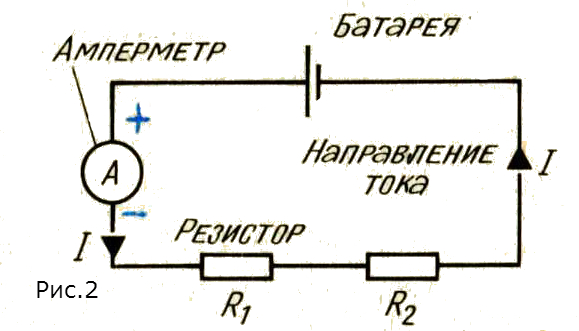
На рисунке 2 показана цепь, в которой все составляющие части соединены последовательно. Это означает, что заряд может перемещаться лишь в одном направлении, и поэтому ток одинаков по всей цепи. Прибор, измеряющий силу тока в цепи, называется амперметром. Он всегда включается в цепь последовательно. Прибор, измеряющий разность потенциалов, называется вольтметром. Он всегда включается в цепь параллельно. Электрическая цепь представляет собой замкнутый путь, по которому течет заряд от одного выхода источника напряжения к другому. На рисунке 3 показана цепь, в которой некоторые компоненты, например два резистора и вольтметр, соединены параллельно.
В точке М цепь разветвляется на три участка, которые может избрать заряд, заряд перераспределяется также и в точке N. Вольтметр измеряет разность потенциалов между точками N и М.
Амперметр и вольтметр имеют выводы, обозначаемые или « + », или «—». Вы должны всегда соединять « + » вывода с положительным выводом батареи. Если подключить наоборот, то чувствительная катушка внутри его будет, вероятно, повреждена и прибор будет испорчен.
Третьим применяемым прибором является гальванометр с установкой на нуль, который показывает направление тока. Он практически является миллиамперметром (очень чувствительным амперметром) с нулевым положением указателя в центре шкалы.
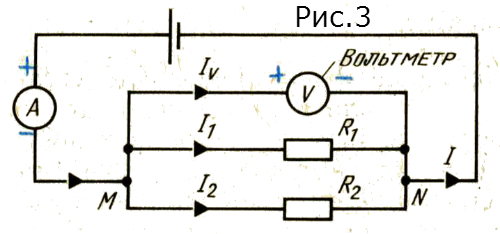
Первый закон Кирхгофа
Этот закон утверждает, что «заряд, входящий во всякое соединение в цепи, должен быть равен заряду, выходящему из этого соединения». Следовательно, в соединении М (рис. 3) заряд, входящий в него за одну секунду, равен заряду, выходящему из него за секунду, т. е.
в точке М IM = I 1+ I2 + Iv,
в точке N I1 + I2 + Iv=IN,
и, следовательно, Iм = IN. Если заряд, который вошел в соединение, больше, чем тот, который из него вышел, то на этом соединении произойдет на то будет иметь место недостаток закопление заряда. И наоборот, если ряда. Очевидно, что ни то, ни другое больший заряд вышел из соединения, невозможно.







