
Новый Эталон Килограмма
может в ближайшее время заменить устаревший платиново-иридиевый... »»»

Солнце Становится Ближе
получены изображения высокого разрешения Солнца с космической обсерватории Solar Dynamics Observatory... »»»

Человек "Искрививший" Время
биография Альберта Эйнштейна - величайшего физика создавшего "Общую теорию относительности"... »»»

Что за Очки у Будущего?
история создания, развития и будущее популярного оптического прибора... »»»
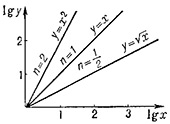
Одним из способом решения задач, связанных с динамикой, является представление движения тела графически. Ниже представлены графики, которые показывают движение различных частиц, подчеркивают векторный характер перемещения, скорости и ускорения.
Обратите внимание, что график «перемещение — время» может быть представлен или непрерывной, или штриховой линией в зависимости от того, какое направление принято за положительное. Если изображаются не векторные, а скалярные величины пройденного расстояния, скорости и быстроты изменения скорости du / dt, то нужно показывать лишь положительную часть графика.
Частица, движущаяся с неизменной скоростью в определенном направлении
Как и ранее, графики, изображающие зависимости расстояния от времени, скорости от времени и быстроты изменения скорости от времени, будут представлять собой положительную часть графика, приведенного на рисунке.
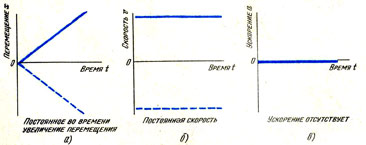
Пример
Мяч брошен вниз с вершины скалы без начальной скорости. В соответствующих графиках, показанных на рисунке 5.5, вершина скалы принята за исходную (нулевую) точку, а направление вверх за положительное. На рисунке 5.6 показаны графики зависимости величин от тех же величин в скалярной форме. Заметьте, что графики для скалярных и векторных величин принципиально отличны.
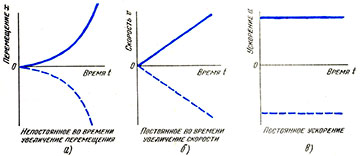
Пример
Мяч, брошенный вертикально вверх со скоростью и с вершины скалы высотой h, падает на расположенный внизу пляж. На этот раз давайте примем пляж за исходный (нулевой) уровень и направление вверх, как и прежде, за положительное. Графики движения показаны на рисунке а, а три соответствующих графика для скалярных величин — на рисунке б.
Теперь должно быть ясно, что построение графиков зависимости перемещения, скорости, ускорения в векторной форме от времени дает больше полезной информации, чем изображение графиков для соответствующих скалярных величин.







