В качестве примера предлагается сле­дующее описание метода проведения эксперимента по закону Гука.

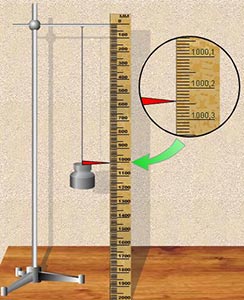Прибор был установлен так, как показано на схеме. До того как к пружине был подвешен какой-либо груз L, было отмечено и записано по­ложение стрелки на линейке. Это по­ложение стрелки взято в качестве ус­ловного нуля. Груз весом 0,5 Н был подвешен к концу пружины. Он в те­чение некоторого времени колебался, затем установилось равновесие, при котором было отмечено новое поло­жение стрелки, и показание занесено в таблицу результатов. Далее добав­лялись грузы весом по 0,5 Н до тех пор, пока вес груза не стал равным 3,0 Н. При этом отмечались показания стрел­ки для каждого груза после установ­ления состояния равновесия. Затем вес груза уменьшался равными час­тями по 0,5 Н, и также отмечались и записывались показания неподвиж­ной стрелки. Усредненные показания стрелки для каждого груза были под­считаны путем сложения показаний при последовательных нагружении и разгружении и деления на 2. Рас­тяжение е пружины было подсчитано для каждого груза путем вычитания показания стрелки для нулевого поло­жения груза из усредненного показа­ния стрелки для каждого груза.

График, показывающий зависи­мость растяжения е от веса груза L в системе прямоугольных координат, и подтверждает прямо пропорциональ­ную зависимость е от L.

Результаты. Таблица результатов была подробно обсуждена на ранее.

Вычисления. Математические вы­числения должны быть полностью представлены в вашей специальной тетради, предпочтительно вместе с таблицей результатов или вблизи нее так, чтобы работа могла быть про­верена учителем. В физике почти все величины имеют свои единицы  измерения, и весьма распространенной . ошибкой является, когда их опускают при подсчетах. Соответствующая еди­ница измерения всегда должна присут­ствовать в конечном результате. Если отсутствует единица измерения, как, например, для показателя преломле­ния, выигрыша в силе при исполь­зовании рычага или отношения ско­ростей, тогда считают такую вели­чину безразмерной.

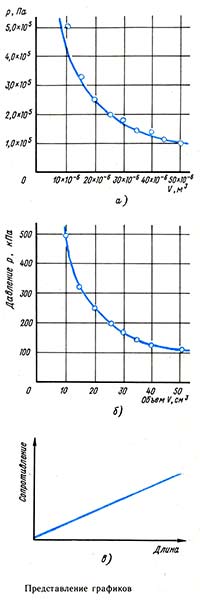График. Графики станут все более и более необходимы по мере того, как вы будете восходить от простого к сложному в изучении физики. Ос­новательная первичная подготовка на этих ранних ступенях весьма важна для любой работы, которую вы впо­следствии выберете. Рисунок 0.2, а демонстрирует рекомендуемый способ обозначения графиков так, чтобы они выглядели как математический ап­парат, имеющий дело только с чис­лами. На оси координат откладывают только числовые значения исследуе­мой величины, единицы измерения которой вынесены на ось вместе с обозначениями величины. На при­веденном рисунке, б)  ось у симво­лизирует давление р, а) х — объем V, однако совсем необязательно исполь­зовать слова «давление» и «объем», так как они уже подразумеваются самими этими символами. Тем не ме­нее в этой книге название величины будет записываться вдоль оси, с тем чтобы помочь вам познакомиться со значениями разнообразных символов. Когда вы поймете значения символов, вы можете при желании опустить сами слова.

На этом уровне позволительно употреблять кратные или дольные еди­ницы измерения, если это упростит числа на графике. Так, например, гра­фик на рисунке 0.2, б мог бы заме­нить график на рисунке 0.2, а, посколь­ку 100 кПа и 50 см³ — более простые для обращения числа, чем 1,0-10⁵ Па и 50- Ю^-6 м выражающие присущие осям единицы измерения. Рекоменду­ется также использование эскизного графика, т. е. такого, который пока­зывает связь между двумя величинами без применения чисел. Рисунок в) демонстрирует пример эскизного гра­фика, на котором показано, что сопро­тивление R проволоки прямо про­порционально длине / этой проволоки. Обратите внимание, что оси обозначены как «сопротивление» и «длина» по названиям исследуемых величин. Символы R и /, а также единицы из­мерения не используются. В качестве упражнения изобразите эскизный график зависимости давления р и объема V для определенной массы га­за при постоянной температуре.

Мы рекомен­дуем, чтобы обозначение и величины используемых шкал добавлялись к тем графикам, которые имеют отношение к экспериментальным или числовым данным. Здесь мы советуем, чтобы каждый график (рис. а) )имел: а) название; б) обозначения обеих осей; в) единицы измерения величин на каждой оси; г) масштабы (шкалы), используемые на каждой оси; д) точки в сочетании с крестиками (X или +) или точки в кружке.

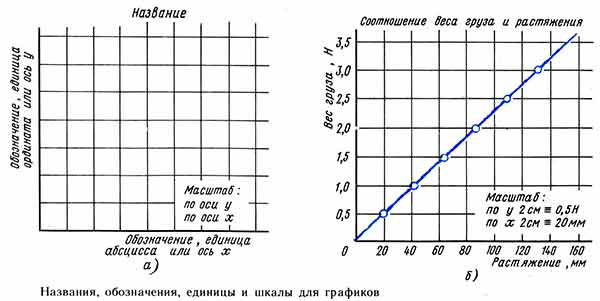
График, изображенный на рисун­ке б), вычерчен по результатам эксперимента по проверке закона Гука. Для акку­ратного проставления точек необходи­ма крайняя тщательность. Точки графика должны быть «связаны» еди­ной прямой линией или дугой. Гра­фик должен занимать как можно боль­шее пространство координатной плос­кости. Для этого необходим разумный выбор масштаба для каждой оси. Вряд ли все точки графика, получен­ные в результате реального экспери­мента, лягут на прямую (или плав­ную кривую) линию вследствие не­избежных погрешностей измерений, поэтому постарайтесь провести пря­мую линию (или плавную дугу) через как можно большее число точек или же так, чтобы распределение точек справа и слева от линии было при­мерно равным. Удобный способ полу­чения сбалансированного графика этого типа показан на рисунке ниже.

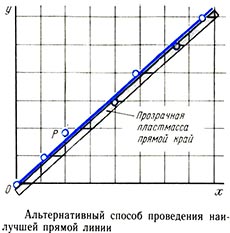Предположим, вам нужно вычертить наилучшую прямую линию, проходя­щую через шесть точек, обозначенных на рисунке 0.4, а. Отметьте (другим цветом или обозначением) промежу­точные точки для каждой пары экспе­риментальных точек, изображенной на графике. Эти пять промежуточных то­чек обозначены знаком « + » на рисун­ке 0.4, б. Промежуточные точки обыч­но лежат очень близко к прямой линии. Таким образом, соединение этих пяти промежуточных точек на рисунке 0.4, б прямой линией дает наилучшую пря­мую линию, проходящую через исход­ные шесть точек. Если же промежу­точные точки не лягут на прямую линию, то процедура может быть по­вторена путем проставления промежу­точных точек для предыдущих промежуточных точек и т. д., пока не бу­дет получена прямая линия.

Другой способ построения для точек, которые не все лежат на прямой линии, состоит в применении узкой прозрачной пластмассовой пластины с ровным краем (например, разме­ром 30X2 см). Поместите пластину поверх точек, как показано на ри­сунке, таким образом, чтобы они на глаз располагались поровну выше и ниже ровного края. Это возможно, по­тому что вы можете видеть эти точки под ровным краем через прозрачную пластину. Затем прочертите прямую линию вдоль ровного края.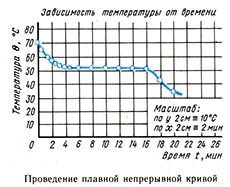
Этот рисунок также демонстрирует другую часто встречающуюся труд­ность при вычерчивании графика, а именно, как следует поступить с точкой Р, которая располагается до­статочно далеко вне прямой линии, проходящей через другие пять точек. В этом случае вы должны отнестись к точке Р как к ошибке и не вклю­чать ее в рассмотрение при проведе­нии прямой линии, а вместо этого выяснить, почему эта точка ошибоч­на. Для того чтобы определить, по­чему точка Р является ошибочной: а)    проверьте,   точно   ли   поставлена эта точка; б) проверьте вычисления для точки Р; в) проверьте прибор; г) если возможно, повторите измере­ния, которые дали точку Р.