Монохроматический свет

На рисунке а показаны лучи, падающие и выходящие перпендикулярно по отношению к решетке. Когда на их пути помещается собирающая линза, то они собираются в фокусе линзы, т. е. в точке О. Все они находятся в одинаковой фазе и поэтому усиливают друг друга при встрече, образуя яркий пучок света. На рисунке б показаны такие же лучи, выходящие под углом b по отношению к решетке. Ширина каждой щели в решетке составляет а, а ширина каждой светонепроницаемой части - b. Их сложение позволяет заметить из геометрических соображений, что λ/(а+ b) = sinθ₁.

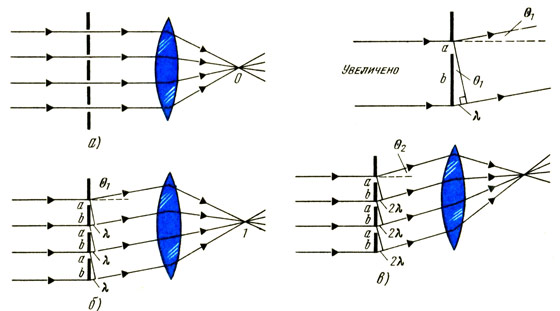
Показаны лучи, которые исходят от верхнего края каждой щели, и каждый луч должен пройти на одну длину волны (λ) больше, чем располагающийся над ним. Нижний луч проходит на три длины волны больше, чем верхний луч, и все эти лучи находятся в фазе. Когда они достигают линзы, они продолжают оставаться в фазе, поскольку разность пройденных расстояний между последующими лучами составляет λ. Поэтому, будучи собранными в фокусе линзой, все они взаимоусилятся и дадут второй яркий пучок.

На рисунке в показаны лучи, исходящие под углом θ₂, таким, что sin θ₂ = 2λ/(а + b). Разность хода между последующими лучами составляет 2λ. И снова лучи взаимоусиливаются, когда фокусируются линзой. Подобным же образом если разность хода составляет три длины волны, то 3λ = (a + b) sin θ₃. В общем виде уравнение разности хода может быть записано как nλ = (a + b) sin θ_n, где n = 0,1,2,3 и т.д. Щели (шириной а) должны быть весьма близки друг к другу (расстояние b мало), 600 штрихов на миллиметр вполне обычное дело. В этом случае (a + b) = ¹/₆₀₀ мм или 10^-3/600 м. 

Расстояние a + b = d называется периодом решетки. Уравнение, связывающее период, следующее: d sin θ = nλ.

Когда монохроматический свет падает нормально на решетку, а проходящий через решетку свет проходит через линзу, то образуются яркие пучки света, как показано на рисунке. Средний пучок соответствует n = 0, а второй пучок с каждой из сторон соответствует n = 2.

Белый свет

Если белый свет проходит через дифракционную решетку, то центральный яркий пучок остается белым. Вместе с тем  поскольку углы отклонения несколько различаются для лучей каждого отдельного цвета, то вместо ярких пучков одного цвета, образованных монохроматическим светом, формируется спектр. Спектр при n = 1 называется спектром первого порядка, а при n = 3 - спектром третьего порядка.

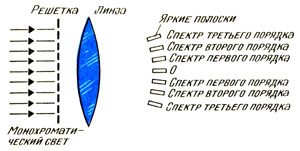Спектр, формируемый дифракционной решеткой, отличается от спектра, образуемого призмой, тем, что цвета здесь располагаются в обратном порядке. Лучи красного цвета - с наибольшей длиной волны - отклоняются решеткой в наибольшей степени, в то время как призмой они отклоняются в наименьшей степени. Решетки чаще используются для образования спектра, чем призмы, потому что дают более широкое его разложение. Ширина спектра увеличивается с повышением порядка.

Можно показать действие дифракционной решетки и с трехсантиметровыми электромагнитными волнами. Для этого случая решетка изготавливается из ряда алюминиевых листов шириной примерно 8 см, разделенных промежутками примерно 2 см. Перед решеткой помещается передатчик, за ней перемещается зонд. Положения максимальной интенсивности звука показывают различные порядки спектров.