
Новый Эталон Килограмма
может в ближайшее время заменить устаревший платиново-иридиевый... »»»

Солнце Становится Ближе
получены изображения высокого разрешения Солнца с космической обсерватории Solar Dynamics Observatory... »»»

Человек "Искрививший" Время
биография Альберта Эйнштейна - величайшего физика создавшего "Общую теорию относительности"... »»»

Что за Очки у Будущего?
история создания, развития и будущее популярного оптического прибора... »»»
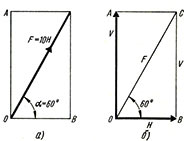
Если две силы могут быть заменены одной результирующей силой, то и одна сила может быть разделена на две силы, действующие под каким-то определенным углом между ними. Если, как часто полагают, угол между этими двумя составляющими силами равен 90°, то это разделение называют как разложение силы на две составляющие под прямым углом. Например, сила 10 Н, действующая под углом α - 60 к горизонту, может быть разложена на две составляющие под прямым углом, например горизонтальную и вертикальную.
Рисунок а показывает эскизную диаграмму силы F — 10 Н, действующую под углом 60° к горизонту, и рисунок б — две составляющие V и Н, действующие в вертикальном и горизонтальном направлении соответственно. Треугольник ОВС дает возможность тригонометрически подсчитать V и Н.
sin α = V/F
F sin α = V
V = 10 sin 60°
V = 10 х 0,8660
V = 8,66 Н
cos α = H/F
F cos α = Н
Н= 10 cos 60°
Н= 10 х 0,5
Н = 5 Н
Для удобств вычисления составляющих нужно запомнит, что составляющая под углом α к силе F всегда равна F cos α или разлагаемая сила определяется косинусом угла между этой силой и ее составляющей. Тогда другая составляющая — это F sin α.
Сила может быть разложена на две составляющие путем изображения в системе координат. Начните с изображения данной одной силы, а затем постройте четырехугольник, диагональю которого является эта сила.
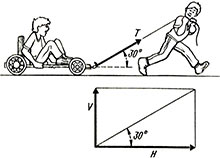
Рассмотрим новости дня, мальчик тянет своего друга, сидящего на тележке, за веревку, направленную под углом 30° к горизонтали (см. рис.). При силе натяжения Т веревки, равной 200 Н, определить:
а) силу, необходимую для движения тележки;
б) силу, стремящуюся поднять тележку с земли.
Разлагаем силу Т = 200 Н на горизонтальную составляющую Н и вертикальную составляющую V:
Н = Т cos 30°
Н = 200 cos 30°
Н = 173 Н
V = Т sin 30°
V = 200 sin 30°
V= 100 Н







