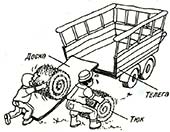Еще один простой «механизм» — это наклонная плоскость. Рисунок показывает фермера и его сына, грузящих тюки соломы в телегу. Фермер поднимает тюк вертикально вверх и кладет в телегу, а его сын использует для погрузки деревянную доску как наклонную плоскость. Фермер должен приложить силу, по меньшей мере равную весу тюка W. Сын же прилагает силу Е = W sin θ + F, где F — сила трения между тюком и доской. Для «малых» углов 8 (до 30°) sin θ меньше 0,5, и отсюда Е меньше W. Поэтому если сын физически не в состоянии непосредственно положить тюк в телегу, как его отец, то он сможет закатить его вверх по наклонной доске.

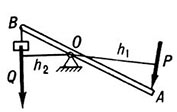Одним из важных практических применений моментов сил относительно точки являются простые «механизмы», такие, как рычаг. «Механизмы» здесь — это любое приспособление, позволяющее силе, приложенной в одной точке, уравновесить или преодолеть другую силу в другой точке. Приложенная сила называется усилие Е, а сила, которую «механизм» должен преодолеть, известна как нагрузка L.

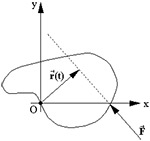Характерным проявлением действия пары сил является отклонение тела от прямолинейного движения, которое можно придать мячу в таких играх, как футбол, крикет, теннис, настольный теннис и гольф. Чтобы заставить мяч двигаться по прямой линии, прилагаемая сила F должна действовать через центр тяжести G мяча, как показано на рисунке а. Чтобы мяч отклонился от прямолинейного движения, сила F может быть приложена в любой точке, кроме G. На рисунке б сила F приложена к нижнему краю мяча. Это заставляет мяч вращаться против часовой стрелки и двигаться вперед.

Принцип действия простых рычажных весов, используемых для сравнения масс тел, может быть продемонстрирован при помощи прибора в исследовании ниже. Снова линейка уравновешена горизонтально на опоре, помещенной в центре тяжести G. Удобно иметь точку G на пятидесятисантиметровой отметке, и этого можно добиться, при необходимости «нагрузив» линейку маленькими шариками пластилина. Тело, массу то которого нужно определить, помещается в какой-либо точке О справа от G и ее расстояние от G записывается в таблице результатов.

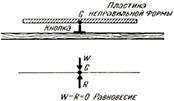Возьмем пластину неправильной формы из листа любого материала одинаковой толщины, например картона, фанеры, пластика и т. д. Просверлим в ней три отверстия (h₁, h₂ и h₃) по краям и под углом примерно 120° друг к другу, если вершину углов расположить примерно в центре пластины. Если предполагается использовать пластину более одного раза, нужно заклеить большую часть площади между h₁, h₂ и h₃ и бумагой. Установим ось (воткните иглу в пробку, которая зажата на подставке, как показано на рисунке а и подвесим пластину на ось через отверстие h₁. Затем на оси (игле) установим отвес — груз на нитке. Слегка отклонимпластину и отпустим ее. Позволим ей колебаться (раскачиваться) свободно, пока она не придет в состояние покоя.

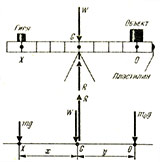
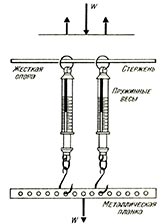На длинном металлическом стержне подвесьте двое пружинных весов, а к весам подвесьте металлическую планку с отверстиями, просверленными через равные интервалы, как показано на рисунке. Изменяйте положение стержня и расстояние между пружинными весами, снимая показания весов для каждого положения. Где бы ни находился стержень — сумма показаний весов равна весу W металлической планки.
При однородной металлической планке весом W возможно, что: а) каждые из пружинных весов покажут вес W/2; б) пружинные весы покажут неравные части W; в) одни весы покажут значение W, другие 0. Даже если подвесить на металлическую планку дополнительные грузы, то показания весов засвидетельствуют, что сумма сил, направленных вверх, всегда равна сумме сил, направленных вниз, и сумма моментов сил относительно любой точки равна нулю.

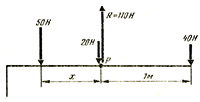Для уравновешивания качелей мальчик должен передвинуться по доске по направлению к бревну. Чтобы подсчитать точно, где он должен сесть для приведения доски в равновесие, изобразите новую диаграмму, как на рисунке 8.10, и определите моменты сил относительно точки Р.

Моменты сил относительно точки Р = + 50 Н х X м + 20 Н x 0 м - 110 Н х 0 м - 40 Н х 1 м = 50х - 40 Нм

Отсюда х находится в 0,8 м от точки Р.